Game Theory - Location Model

Each and every one of us has definitely encountered the term “Game theory” somewhere or the other, in our lives. But what is it, exactly? In simple terms, game theory is the study of conflicts and cooperation that occurs among rational participants in a competitive situation, through mathematical models. The term ‘game’ can be a bit misleading, but pretty much any interactive situation with rules, participants (or players) decisions and consequences can be called a game. Basically, in game theory, a real-world or hypothetical situation is turned into a mathematical puzzle to analyze the decisions made by each player and the overall outcome. Game theory has an incredibly wide range of applications in every field, be it biology, philosophy, computer science, political science or economics. It can be used to explain a wide range of phenomenon which we experience in our daily lives. In this article, I’ve discussed just one such real-world application to illustrate the scope of game theory.

The spatial competition problem:

Have you ever noticed how mobile phone showrooms, automobile showrooms, fast food joints etc always seem to exist in clusters together? Or when you are looking for a hardware shop and you can't seem to find a single one, but then all of a sudden you see five or six of them in a single neighbourhood, right next to each other? Does it ever make you wonder why they don't just spread out across the city so they are no longer reducing each other’s consumer share, which would be better for all of them? It doesn’t seem to make any sense, and yet it occurs everywhere!

To explain this phenomenon, we use a game theory instrument known as the location model. A location model analyses the relation between location, pricing strategies of competing firms and resulting consumer preferences. There are two factors a customer considers while choosing the same product from competitor brands - the price of product (p) and travel cost (c) (assuming that there is absolutely no quality difference between the products). The sum of the two, P (P = p+c) determines customer choice, and the firm with lower P is preferred by the consumer. We must also remember that any firm aims to achieve maximum possible profitability and sales. This is considered to be the rational motive of the firm. There are two primary location models- Hotelling’s model, and Salop’s circle model. We use Hotelling’s model in this case as it is less complex.

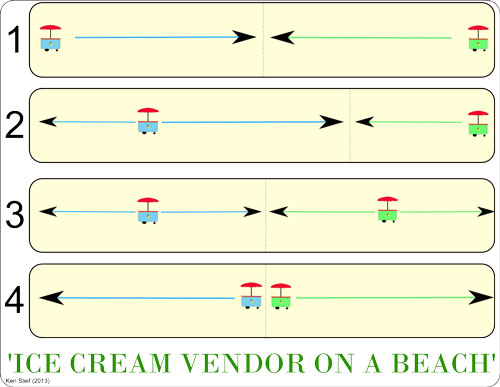
Let us apply this model to a beach. An ice cream stall, A is opened up. Since there is no competition, the owner will place his stall right in the centre as it attracts maximum customers. A few days later, another ice cream stall (B) opens up. There is a natural competition among the two sellers, since the space is limited. Let us assume they mutually agree to set up at opposite corners so that each of them can cover half of the community without affecting the other, a solution which game theorists refer to as the ‘socially optimal solution’ (SOS) , i.e. the ideal solution.

However, the very next day, while A sets up his stall at his corner, B realises that he can set up his stall at the centre and take half of the total consumers plus half of the customers in the second half as well, thus giving him more advantage. When A confronts B about this, he promises not to do it again, but A decides to take revenge. While B sets up at his corner, A sets up just south of B, thus having three fourths of the beach to himself and leaving only one for B. Now B moves his stall just south of A’s, doing the same to A.

This cycle goes on until they are both now at the centre. At this point, neither of them want to go south or north since neither of them have anything further to gain by changing only their own strategy while the other’s remains same. This brings both A and B to a standstill, making it impossible for them to find a more favourable space to set up their stall within the community. This situation is referred to as the Nash equilibrium and is the most stable solution possible.

It is interesting to note here that the most ideal solution fails in this situation as it is unstable, but Nash equilibrium prevails.

Nash equilibrium - definition - The Nash Equilibrium is a situation where neither competitor has any incentive to change their strategy assuming the other’s to be constant.

This is merely one of the innumerable applications of game theory in its limitless scope. The reader is encouraged to read further on this topic and there are several interesting videos available on game theory online as well.

- Kushagra K Chanda